Tích phân

Cách 1: Dựng hình thang

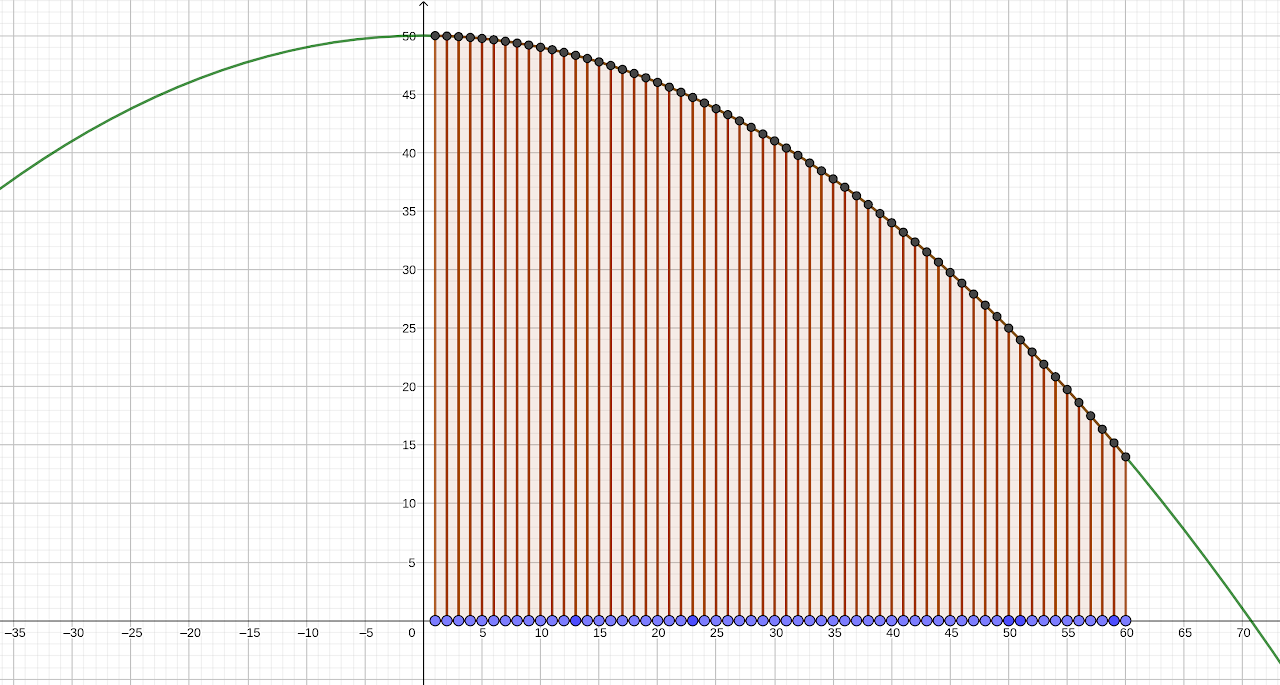
const int STEP = 1e6;
double f(double x) {
    /* function here */
}
double integral(double x1, double x2) {
    double d = (x2-x1)/STEP;
    double S = 0;
    for (int i = 0; i < STEP; ++i) {
        S += (f(x1+i*d)+f(x1+(i+1)*d))*d/2;
    }
    return S;
}

const int STEP = 1e6;
double f(double x) {
    /* function here */
}
double integral(double x1, double x2) {
    double d = (x2-x1)/STEP;
    double S = f(x1) + f(x2);
    for (int i = 1; i < STEP; ++i) {
        S += 2*f(x1+i*d);
    }
    return S*d/2;
}

Cách 2: Simpson’s rule ver 1

const int STEP = 1e6;
double f(double x) {
    /* function here */
}
double integral(double x1, double x2) {
    double d = (x2-x1)/STEP;
    double S = f(x1) + f(x2);
    for (int i = 1; i < STEP; ++i) {
        S += f(x1+i*d) * (i&1?4:2);
    }
    return S*d/3;
}

Cách 3: Simpson’s rule ver 2

const double eps = 1e-12;
double f(double x) {
    /* function here */
}
double simpson(double x1, double x2) {
    return (x2-x1)/6*(f(x1)+f(x2)+4*f((x1+x2)/2));
}
double integral(double x1, double x2, double ans) {
    double m = (x1+x2)/2;
    double lef = simpson(x1,m);
    double rig = simpson(m,x2);
    if (fabs(lef+rig-ans) < eps) return ans;
    return integral(x1,m,lef) + integral(m,x2,rig);
}
double integral(double x1, double x2) {
    return integral(x1,x2,simpson(x1,x2));
}

Tham khảo thêm

Bài tập

Code giải một số bài tập

ellipse 
#include <bits/stdc++.h>

using namespace std;

const double eps = 1e-12;
double a, b;

double f(double x) {
    /* function here */
    return b*sqrt((1-x/a)*(1+x/a));
}
double simpson(double x1, double x2) {
    return (x2-x1)/6*(f(x1)+f(x2)+4*f((x1+x2)/2));
}
double integral(double x1, double x2, double ans) {
    double m = (x1+x2)/2;
    double lef = simpson(x1,m);
    double rig = simpson(m,x2);
    if (fabs(lef+rig-ans) < eps) return ans;
    return integral(x1,m,lef) + integral(m,x2,rig);
}
double integral(double x1, double x2) {
    return integral(x1,x2,simpson(x1,x2));
}

int main() {
    int t; cin >> t;
    cout << setprecision(3) << fixed;
    while (t--) {
        double x1, x2;
        cin >> a >> b >> x1 >> x2;
        cout << integral(x1,x2)*2 << '\n';
    }
    return 0;
}
Enviroment Protection 
#include <bits/stdc++.h>

using namespace std;

const int STEP = 1e3;
const double eps = 1e-6;
double W, D, A, K;

struct Func {
    int k;
    vector<double> a, b;
    void init(int k_) {
        k = k_;
        a.resize(k+1);
        b.resize(k+1);
    }
    friend istream& operator >> (istream&is,Func&f) {
        for (int i = 0; i <= f.k; ++i) {
            is >> f.a[i];
        }
        for (int i = 0; i <= f.k; ++i) {
            is >> f.b[i];
        }
        return is;
    }
    Func operator - (double t) {
        Func tmp = *this;
        for (int i = 0; i <= k; ++i) {
            tmp.a[i] -= t*tmp.b[i];
        } return tmp;
    }
    double eval(double x) {
        double A = 0;
        double B = 0;
        for (int i = 0; i <= k; ++i) {
            A += a[i]*pow(x,i);
            B += b[i]*pow(x,i);
        } return A/B;
    }
    double integralPos(double x1, double x2) {
        double d = (x2-x1) / STEP;
        double S = 0;
        for (int i = 0; i < STEP; ++i) {
            double s = (eval(x1+i*d) + eval(x1+(i+1)*d)) * d / 2;
            if (s > 0) S += s;
        } return S;
    }
} yy1, yy2;

double solve() {
    double up = 0;
    double down = -D;
    while (fabs(up-down)>eps) {
        double m = (up+down)/2;
        double S = (yy1-m).integralPos(0,W)-(yy2-m).integralPos(0,W);
        if (S+eps<A) up = m;
        else down = m;
    }
    return -up;
}

int main() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cout << setprecision(5) << fixed;
    while (cin >> W >> D >> A >> K) {
        yy1.init(K); yy2.init(K);
        cin >> yy1 >> yy2;
        cout << solve() << '\n';
    }
    return 0;
}
Curvy Little Bottles 
#include <bits/stdc++.h>

using namespace std;

const int STEP = 1e3;
const double eps = 1e-6;
double W, D, A, K;

struct Func {
    int k;
    vector<double> a, b;
    void init(int k_) {
        k = k_;
        a.resize(k+1);
        b.resize(k+1);
    }
    friend istream& operator >> (istream&is,Func&f) {
        for (int i = 0; i <= f.k; ++i) {
            is >> f.a[i];
        }
        for (int i = 0; i <= f.k; ++i) {
            is >> f.b[i];
        }
        return is;
    }
    Func operator - (double t) {
        Func tmp = *this;
        for (int i = 0; i <= k; ++i) {
            tmp.a[i] -= t*tmp.b[i];
        } return tmp;
    }
    double eval(double x) {
        double A = 0;
        double B = 0;
        for (int i = 0; i <= k; ++i) {
            A += a[i]*pow(x,i);
            B += b[i]*pow(x,i);
        } return A/B;
    }
    double integralPos(double x1, double x2) {
        double d = (x2-x1) / STEP;
        double S = 0;
        for (int i = 0; i < STEP; ++i) {
            double s = (eval(x1+i*d) + eval(x1+(i+1)*d)) * d / 2;
            if (s > 0) S += s;
        } return S;
    }
} yy1, yy2;

double solve() {
    double up = 0;
    double down = -D;
    while (fabs(up-down)>eps) {
        double m = (up+down)/2;
        double S = (yy1-m).integralPos(0,W)-(yy2-m).integralPos(0,W);
        if (S+eps<A) up = m;
        else down = m;
    }
    return -up;
}

int main() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cout << setprecision(5) << fixed;
    while (cin >> W >> D >> A >> K) {
        yy1.init(K); yy2.init(K);
        cin >> yy1 >> yy2;
        cout << solve() << '\n';
    }
    return 0;
}
GM-pineapple 
#include <bits/stdc++.h>

using namespace std;

const double eps = 1e-12;
const double PI = acos(-1);
int n;
double a, b;

double f(double x) {
    return b*b*(1-x/a)*(1+x/a);
}

double simpson(double x1, double x2) {
    return (x2-x1)/6*(f(x1)+f(x2)+4*f((x1+x2)/2));
}

double integral(double x1, double x2, double ans) {
    double m = (x1+x2)/2;
    double lef = simpson(x1,m);
    double rig = simpson(m,x2);
    if (fabs(lef+rig-ans) < eps) return ans;
    return integral(x1,m,lef) + integral(m,x2,rig);
}

double integral(double x1, double x2) {
    return integral(x1,x2,simpson(x1,x2));
}

int main() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cout << setprecision(6) << fixed;
    cin >> b >> a >> n;
    double d = a / n;
    a /= 2; b /= 2;
    for (int i = 0; i < n; ++i) {
        cout << integral(-a+i*d,-a+(i+1)*d)*PI << '\n';
    }
    return 0;
}
Stolen 
// public: https://drive.google.com/drive/folders/1yJmkstPMC-BJxrVR5vAhGQH1MB_QJ8Pq?fbclid=IwAR1DPVOCynn1ZEKZ5-2jqhvoXFF7baF7kzkskE95E5o0_F0MwnNuGJSTgD8
// link de: https://drive.google.com/file/d/13f8l02T5nfzRJ7gfX2cIZvNQqq_ZCMT_/view

#include <bits/stdc++.h>
#define Point Vector
#define fi first
#define se second
#define debug(x) cerr << #x << " = " << x << '\n'

using namespace std;

const double eps = 1e-6;
const double PI = acos(-1);
const int STEP = 1e6;

double cub(double x) {
    return x*x*x;
}

double cubr(double x) {
    if (x < 0) return -pow(-x,1.0/3);
    return pow(x,1.0/3);
}

vector<double> FirstDegreeEquation(double a, double b) {
    return {-b/a};   
}

vector<double> QuadraticEquation(double a, double b, double c) {
    double delta = b*b - 4*a*c;
    if (delta < 0) return {};
    if (fabs(delta) <= eps) {
        return {-b/(2*a)};
    }
    double x1 = (-b-sqrt(delta)) / (2*a);
    double x2 = (-b+sqrt(delta)) / (2*a);
    return {x1,x2};
}

vector<double> CubicEquation(double a, double b, double c, double d) {
    double delta = b*b - 3*a*c;
    if (abs(delta) <= eps) {
        double k = b*b*b - 27*a*a*d;
        if (fabs(k)-1 <= eps) {
            return {-b/(3*a)};
        }
        else {
            return {(-b+cubr(k))/(3*a)};
        }
    }
    else {
        double k = (9*a*b*c - 2*b*b*b - 27*a*a*d) / (2*sqrt(cub(fabs(delta))));
        if (delta > 0) {
            if (fabs(k) <= 1) {
                double x1 = (2*sqrt(delta)*cos(acos(k)/3) - b) / (3*a);
                double x2 = (2*sqrt(delta)*cos(acos(k)/3 - 2*PI/3) - b) / (3*a);
                double x3 = (2*sqrt(delta)*cos(acos(k)/3 + 2*PI/3) - b) / (3*a);
                return {x1,x2,x3};
            }
            else {
                double x = sqrt(fabs(delta))*fabs(k)/(3*a*k);
                x *= cubr(fabs(k)+sqrt(k*k-1)) + cubr(fabs(k)-sqrt(k*k-1));
                x -= b / (3*a);
                return {x};
            }
        }
        else {
            double x = sqrt(fabs(delta))/(3*a);
            x *= cubr(k+sqrt(k*k+1)) + cubr(k-sqrt(k*k+1));
            x -= b / (3*a);
            return {x};
        }
    }
}

struct Vector {
    double x, y;
    friend istream& operator >> (istream&is, Vector&p) {
        is >> p.x >> p.y;
        return is;
    }
    friend ostream& operator << (ostream&os, Vector p) {
        os << p.x << ' ' << p.y;
        return os;
    }
    Vector operator - (Vector a) {
        return {x-a.x,y-a.y};
    }
    double operator % (Vector a) {
        return x*a.y - a.x*y;   
    }
    friend bool CWW(Point a, Point b, Point c) {
        return (b-a)%(c-b) > 0;
    }
};

struct func3 {
    double a, b, c, d;
    friend istream& operator >> (istream&is,func3&f) {
        is >> f.a >> f.b >> f.c >> f.d;
        return is;
    }
    friend ostream& operator << (ostream&os, func3&f) {
        os << f.a << ' ' << f.b << ' ' << f.c << ' ' << f.d;
        return os;
    }
    double eval(double x) {
        return a*x*x*x + b*x*x + c*x + d;
    }
    friend Point inter(func3 f, func3 g) {
        double aa = f.a - g.a;
        double bb = f.b - g.b;
        double cc = f.c - g.c;
        double dd = f.d - g.d;
        vector<double> v;
        if (aa==0) {
            if (bb==0) {
                v = FirstDegreeEquation(cc,dd);
            }
            else {
                v = QuadraticEquation(bb,cc,dd);
            }
        }
        else {
            v = CubicEquation(aa,bb,cc,dd);
        }
        vector<Point> res;
        for (double &x : v) {
            res.push_back({x,f.eval(x)});
        }
        return res[0];
    }
    double integral(double x1, double x2) {
        double d = (x2-x1) / STEP;
        double S = 0;
        for (int i = 0; i < STEP; ++i) {
            S += (eval(x1+i*d)+eval(x1+(i+1)*d))*d/2;
        }
        return S;
    }
};

func3 f[3];
vector<pair<Point,int>> v;

int main() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> f[0] >> f[1] >> f[2];
    Point p01 = inter(f[0],f[1]);   
    Point p02 = inter(f[0],f[2]);   
    Point p12 = inter(f[1],f[2]);
    v.push_back({p01,3});
    v.push_back({p02,5});
    v.push_back({p12,6});
    sort(v.begin(),v.end(),[&](pair<Point,int>&a,pair<Point,int>&b) {
        return a.fi.x < b.fi.x;
    });
    cout << setprecision(6) << fixed;

    if (CWW(v[0].fi,v[2].fi,v[1].fi)) {
        func3 f1 = f[int(log2(v[0].se & v[1].se))];
        func3 f2 = f[int(log2(v[1].se & v[2].se))];
        func3 f3 = f[int(log2(v[0].se & v[2].se))];
        double res = f1.integral(v[0].fi.x,v[1].fi.x) - f3.integral(v[0].fi.x,v[1].fi.x);
        res += f2.integral(v[1].fi.x,v[2].fi.x) - f3.integral(v[1].fi.x,v[2].fi.x);
        cout << res << '\n';    
    }
    else {
        func3 f1 = f[int(log2(v[0].se & v[2].se))];
        func3 f2 = f[int(log2(v[0].se & v[1].se))];
        func3 f3 = f[int(log2(v[1].se & v[2].se))];
        double res = f1.integral(v[0].fi.x,v[1].fi.x) - f2.integral(v[0].fi.x,v[1].fi.x);
        res += f1.integral(v[1].fi.x,v[2].fi.x) - f3.integral(v[1].fi.x,v[2].fi.x);
        cout << res << '\n';
    }

    return 0;
}

Lời giải